最近在看Hash有关的文章,打算从头开始看,那就从最简单的部分开始了解吧。参考博客布隆过滤器
Hash函数
$Hash$函数的作用主要是将一个大的数据集映射到小的数据集上,这些小的数据集称作为哈希值或者散列值。$Hash\ Table$(哈希表,散列表)是根据哈希值进行访问的数据结构,也就是说我们通过把哈希值映射到表中一个位置来访问记录,以加快查找的速度。下面是一个典型的$Hash$函数示意图:
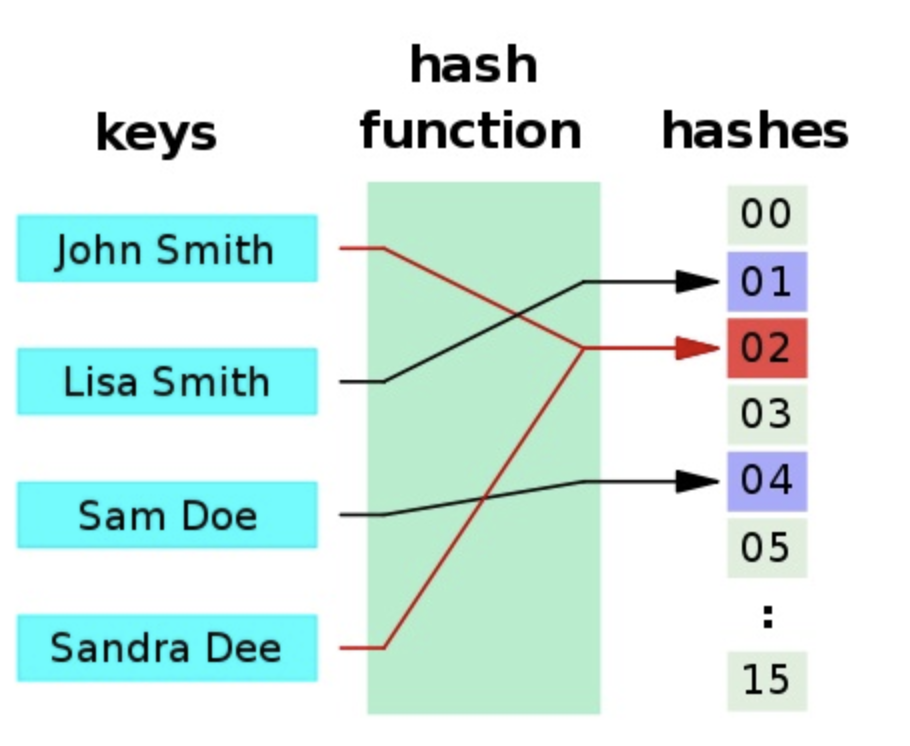
$Hash$函数主要有一下两个特点:
- 对于同一个哈希函数,如果两个数据的哈希值不一样,那么这两个数据肯定不一样
- 哈希函数存在碰撞,两个不一样的$Key$的哈希值可能是一样的,比如上图的$John$和$Sandra$的哈希值都是02
Hash一个应用就是对数据集分类,比如上图,Hash值为0的表示可能在A集合中,Hash值为2的表示B集合中,依次类推,值为15的表示F集合中。但Hash冲突会在这里会导致严重的问题,对于一个未知的新值,其可能不属于上面任何一个集合,但由于冲突,其Hash值和上面的某一个相同,导致误报(因为事先我们不可能做一个含有无限多项输入的完整的Hash表,也就是原来的Hash函数不可能是完美的)。并且,hash冲突也会导致查找效率低下
布隆过滤器
$Bloom\ Filter$是1970年由$Bloom$提出的。它实际上是一个很长的二进制向量和一系列的随机映射函数($Hash$函数).布隆过滤器可以用于检索一个元素是否在一个集合中。它的优点是空间效率和查询时间都远远超过一般的算法,缺点是有一定的误识别率和删除困难.对于一个大小为$m$的哈希表,要想它的冲突率为$1\%$,那么这个哈希表的元素最多为$\frac{m}{100}$,可以这样子理解,假设现在有$x$个元素,那么对于一个$key$,它冲突的概率为$\frac{x}{m}$,(这里假设只有一个哈希函数)。然而这样子的话空间利用率就不够了,布隆过滤器的解决方案就是使用多个$Hash$函数。
一个$Bloom\ Filter$是基于一个m位的位向量($b_1,…b_m$),这些位向量的初始值为0。另外,还有一系列的hash函数($h_1,…h_k$),这些$hash$函数的值域属于1~m。下图是一个$bloom\ filter$插$x,y,z$并判断某个值$w$是否在该数据集的示意图:
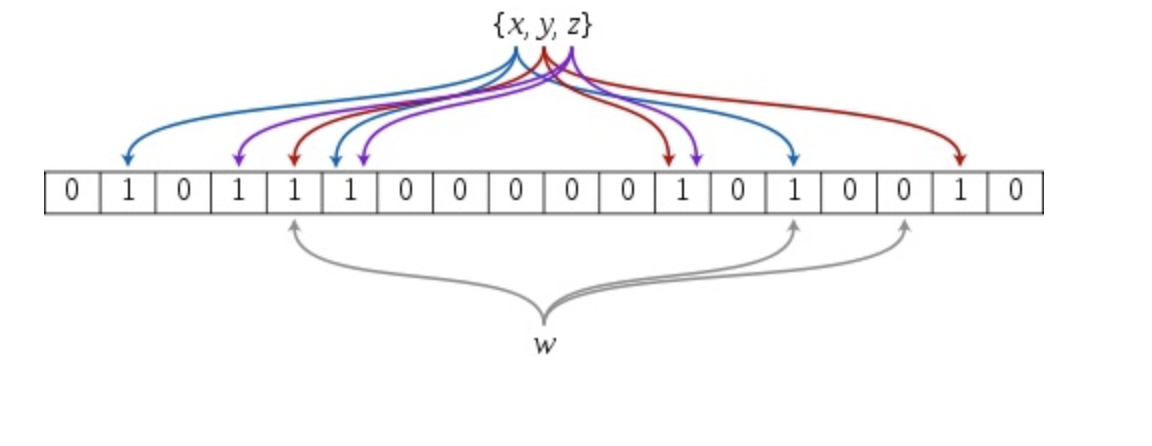
上图中,$m=18,k=3$;插入x是,三个hash函数分别得到蓝线对应的三个值,并将对应的位向量改为1,插入$y,z$时,类似的,分别将红线,紫线对应的位向量改为1。查找时,当查找x时,三个$hash$值对应的位向量都为1,因此判断$x$在此数据集中。$y,z$也是如此。但是查找$w$时,$w$有个$hash$值对应的位向量为0,因此可以判断不在此集合中。但是,假如$w$的最后那个$hash$值比上图中的大1,这是就会认为$w$在此集合中,而事实上,w可能不在此集合中,因此可能出现误报。显然的,插入数据越多,1的位数越多,误报的概率越大。误报概率和$k$的大小有关系,误报概率证明参考误报概率分析(我在下一篇博客,布谷鸟过滤器也提供了一下简单的证明,用于比较)
可以看出布隆过滤器有以下几个特点
- 不存在漏报,某个元素在某个集合中,肯定可以报出来
- 可能存在误报,假阳性。某个元素不在某个集合中,可能也报出来
- 确定某个元素是否在某个集合中的代价和总的元素数目无关。
优点
相比于其它的数据结构,Bloom Filter在空间和时间方面都有巨大的优势。Bloom Filter存储空间和插入/查询时间都是常数。另外, Hash函数相互之间没有关系,方便由硬件并行实现。Bloom Filter不需要存储元素本身,在某些对保密要求非常严格的场合有优势
缺点
一般情况下不能从Bloom Filter中删除元素. 我们很容易想到把位列阵变成整数数组,每插入一个元素相应的计数器加1, 这样删除元素时将计数器减掉就可以了。然而要保证安全的删除元素并非如此简单。首先我们必须保证删除的元素的确在Bloom Filter里面. 这一点单凭这个过滤器是无法保证的。另外计数器回绕也会造成问题。