这篇论文提出了一个新的过滤器-布谷鸟过滤器,相对于布隆过滤器来说达到相同的假阳性率(小于$3\%$),Cuckoo Filter的容量利用率以及失败查找次数等属性都更加优越。这篇博客主要记录一下Cuckoo的一些特性,以及简单的公式推导。
1.Cuckoo Hash
$Cuckoo\ Hash$有两个$Hash$函数,对于一个$Item$我们可以计算出两个位置$a,b$,我们随机选择一个位置去存储,这里的话我们选择$a$。当另一个$Item$需要插入的时候,比如它的位置是$a,c$,并且位置$c$已经有数据了。那么会将$a$中的数据迁移到$b$中,然后再将这个$Item$插入$a$。这样就解决了一次冲突。
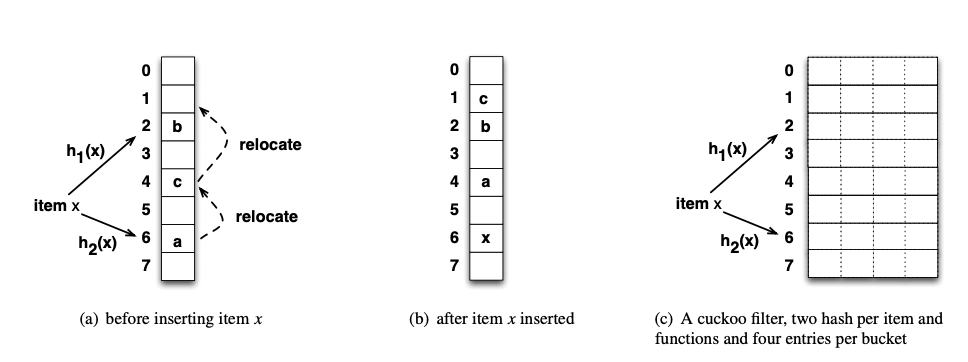
图$c$展示了$Cuckoo\ Filter$的基本结构,这里的配置是每一个$bucket$都有四个$entry$。
2.Cuckoo Filter
作为过滤器,保持小的空间是很有必要的。Cuckoo主要有两个挑战
- 只存储$Key$的指纹,而不存储完整的$Key$
- 对于每一个$Item$有多个关联的位置,在一定程度上会提高$Hash\ Table$的占用率,但是也会提高假阳性率$\epsilon$,同时也会要求更高的$fingerprint$,三者之间的平衡需要进行一个仔细的推敲
对于挑战1,$Cuckoo\ Filter$通过异或操作来实现。对于一个$Item\ x$,作者提供的$Hash$函数如下
\[\begin{align} h_1(x)&=hash(x)\tag 1\\ h_2(x)&=h_1(x)\bigoplus hash(x's\ fingerprint)\tag 2 \end{align}\]为什么不是直接异或指纹,而是要Hash一次。假设指纹我们只取低8位,那么h2(x)的值顶多相对于h1(x)来说就改变了256,因为高位都为0,不会发生改变,这样子的话两个位置就太过集中,容易导致冲突。因此进行一次Hash
这样子的$Hash$函数对于任何一个位置,需要得到另一个位置的信息,只需要在进行一次异或$Hash(x’s\ fingerprint)$的操作即可。假设现在一个位置为$i$,那么得到另一个位置的方法为
\[j=i\bigoplus{hash(x's\ fingerprint)}\]2.1Insert
插入需要考虑到移动操作的上线,防止陷入死循环。一般需要设置一个移动上限($MaxNumKicks$)。

2.2Lookup
查找函数,只需要查找这两个位置对应的条目是否包含这个指纹,有的话返回$True$,没有的话返回$False$

2.3Delete
删除操作查看这两个位置哪个位置包含这个指纹,找到了的话就删除

2.4 局限性分析
$CucKoo$还是具有一定的局限性,假阳性的问题依然存在,对于两个$Item$可能存在$Hash$一样并且指纹也一样的概率,这样子的话可能存在误删的概率,从而导致误报,我们能做的就是在理论上让这样子的情况低于某一个百分比。
3.ASYMPTOTIC BEHAVIOR
主要分析插入失败的概率
下面的表格展示一些公式推导所需要的变量和含义
\[\begin{array}{cc} \hline \epsilon&&target\ false\ positive\ rate&&\\ f&&fingerprint\ length\ in\ bits\\ \alpha&&load\ factor (0 ≤ α ≤ 1)\\ b&&number\ of\ entries\ per\ bucket\\ m&&number\ of\ buckets\\ n&&number\ of\ items\\ C&&average\ bits\ per\ item\\ \hline \end{array}\]首先来设想一下,如何才会插入失败,那就是$2b+1$个$key$,这些$key$的$h_1(x)$和$h_2(x)$都是一样的。我们这里假设$Hash(x’s\ fingerprint)$是一个不会发生冲突的函数。假设现在$x$两个桶的位置是$l_1,l_2$。对于$y$来说要和$x$发生冲突,那么指纹肯定需要一样,指纹一样的概率为$\frac{1}{2^f}$,指纹一样的话,$y$要被映射到桶$l_1,l_2$都可能会发生冲突,这样的概率为$\frac{1}{m}+\frac{1}{m}$,也就是$\frac{2}{m}$。对于$n$个数据,只要有$2*b+1$的数据发生冲突,那么就会发生插入失败,这样子的组合为$\tbinom{n}{2b+1}$所以失败的概率为
\[\tbinom{n}{2b+1}(\frac{2}{2^f\cdot{m}})=\tbinom{n}{2b+1}(\frac{2}{2^f\cdot{cn}})=Ω(\frac{n}{4^{bf}})\]这样字看起来失败概率为$\Omega(n)$,理想情况应该为$\Omega(1)$,那么$4^{bf}$应该为$\Omega(n)$,那么$f=\Omega(log\frac{n}{b})$。
这样看起来$f$的长度跟着$n$变化,但是只要我们将$b$保持在一个稳定的大小,那么$f$就可以取比较小的值。

- Larger buckets improve table occupancy
- Larger buckets require longer fingerprints to retain the same false positive rate
- Optimal bucket size

4.Cuckoo Filter Vs Bloom Filter
这里给出表格,这一章主要是进行公式推导(表格中的数据,默认b=4)

4.1 Cuckoo
假阳性率假设为$\epsilon$,如何出现假阳性率,那就是有两个数字本身不一样,但是指纹一样。可能返回假的指纹。对于查找操作,我们最多最多比较$2b$次。这$2b$次的假阳性率等于1减去查找不到的概率。这$2b$个数字都不是这个指纹的概率为$(1-2^f)^{2b}$.所以假阳性率最高为
\[1-(1-2^f)^{2b}\approx\frac{2b}{2^f}\]我们要求这个概率小于$\epsilon$,那么就是$\frac{2b}{2^f}\leq{\epsilon}$,也就是
\[\begin{align} f&\geq\lceil{log_2(\frac{2b}{\epsilon})}\rceil \\ &\geq\lceil{log_2\frac{1}{\epsilon}+log_22b}\rceil \end{align}\]对于$C(bits\ per\ item)$有
\[C=\frac{哈希表大小}{占用的条目数}=\frac{f*所有的条目}{\alpha*所有的条目}\ \ \ \ =\frac{f}{\alpha}\]这里的话作者给出了一个空间的小的优化,称作为$semi-sort$,这里简单的提一下。假设一个$buckets$有4个$entrys$,每个条目的$fingerprint$为4位,那么这个$buckets$就是16位。每个位置上可以表示16个数。假设这4个$e$ntrys是排序好的,有多少种情况。这个相当于从16个数里面选出四个排序好的数,有多少种情况,这个称作为combinations with replacement.公式为
\[C_n^r=\frac{(n+r−1)!}{r!(n−1)!}\]代入$n=16,r=4$,这样子的话算出来一共就3876种情况。我们用一个12位就可以表示这么多情况。这样子的相当于每一个条目减少了一位,所以表格里优化的方案的$C$为$(log_2(\frac{1}{\epsilon}+2))$
4.2 Bloom
下面来推导布隆过滤器的$C$,同样的假阳性率为$\epsilon$,布隆过滤器的哈希函数个数为$k$,$m$为一共多少位。参考链接先放上
假设现在对于任何一个位置,它不被某个哈希函数置为1的概率为
\[1-\frac{1}{m}\tag 1\]现在有k个函数,它不被置为一的概率为
\[(1-\frac{1}{m})^k\tag 2\]对于极限
\[{\displaystyle \lim _{m\to \infty }\left(1-{\frac {1}{m}}\right)^{m}={\frac {1}{e}}}\tag3\]所以$2$式可以变为
\[(1-\frac{1}{m})^k={\displaystyle \left(1-{\frac {1}{m}}\right)^{k}=\left(\left(1-{\frac {1}{m}}\right)^{m}\right)^{k/m}\approx e^{-k/m}}\tag 4\]假设现在我们插入$n$个数据,这一位还是0的概率为
\[{\displaystyle \left(1-{\frac {1}{m}}\right)^{kn}\approx e^{-kn/m}\tag 5}\]那么这一位为1的概率为
\[{\displaystyle 1-\left(1-{\frac {1}{m}}\right)^{kn}\approx 1-e^{-kn/m}\tag 6}\]现在新插入一个数字,出现假阳性,那么就是需要k个位置都是1,概率为
\[{\displaystyle \varepsilon =\left(1-\left[1-{\frac {1}{m}}\right]^{kn}\right)^{k}\approx \left(1-e^{-kn/m}\right)^{k}\tag 7}\]可以看出$m$越大,假阳性率越低,$n$越大假阳性率越高。
k就是我们哈希函数的数量,也就是一次查找操作需要访问的位的数量,那么k为什么值的时候,$\epsilon$最小呢,求导,把$n$和$m$当做常数,k为变量进行求导.求导过程参考博客。
当$k=ln2\cdot\frac{m}{n}$,可以达到最小的误判率
\[\begin{align} \epsilon&=2^{-k}\tag 8\\ k&=log_2{\frac{1}{\epsilon}}\tag 9 \end{align}\]下面求$C$,对于$n$和$\epsilon$这两个值是已经知道的,首先我们求$m$,
\[m=-\frac{n\cdot\ln\epsilon}{(ln2)^2}\]布隆过滤器里面
\[\begin{align} C&=\frac{m}{n}\\ &=-\frac{\ln\epsilon}{(ln2)^2}\\ &=1.44\cdot\log_2{\frac{1}{\epsilon}} \end{align}\]所以就这样子的出来了内存占用,并且访问次数为$k$,当查找失败的时候,对于误判率最低的布隆过滤器,它的空间占用率为50%.所以最差的搜索失败的次数为2.查找两个位置,一个为0一个为1就返回失败的结果。 当$k = 0.7\frac{m}{n }$,,误判率$\epsilon$最低,此时
\[\begin{align} \displaystyle 1-\left(1-{\frac {1}{m}}\right)^{kn}&\approx 1-e^{-kn/m}\tag 6\\ &\approx1-e^{-0.7}\\ &\approx0.5 \end{align}\]此公式意义为:若插入了$n$个元素,该位仍然没有被置“1”的概率,也就是说想保持错误率低,布隆过滤器的空间使用率需为50%
5.Advantage
-
It supports adding and removing items dynamically;
-
It provides higher lookup performance than traditional Bloom filters, even when close to full (e.g., 95% space utilized);
-
It is easier to implement than alternatives such as the quotient filter; and
-
It uses less space than Bloom filters in many practical applications, if the target false positive rate ε is less than 3%.